問1 線形探索
線形探索は、最初のデータから順番に1つずつ一致するのか見ていくというものです。
問題文では、後に「順次法」と表現されています。
質問を図で表すと、次のようになります。
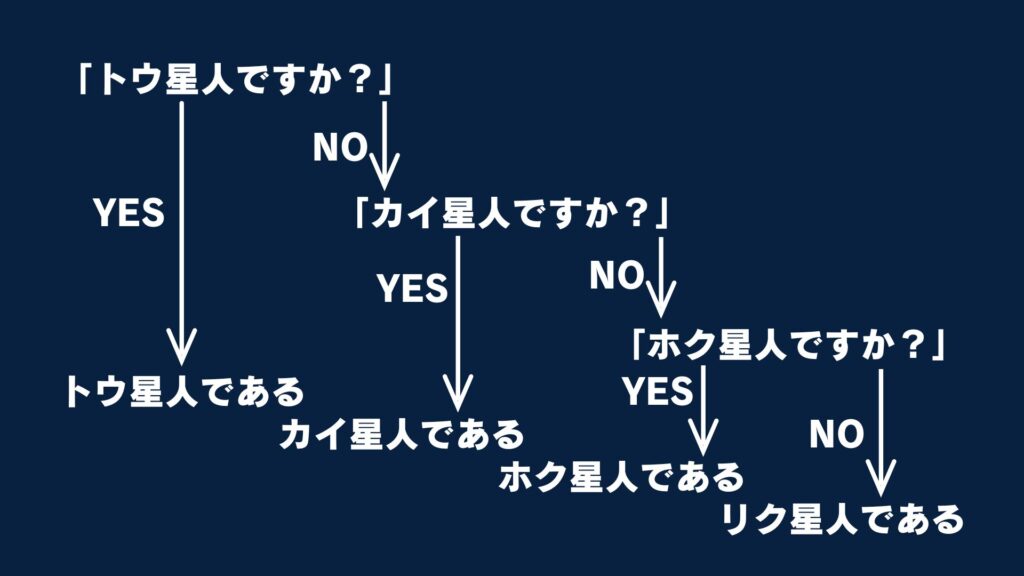
リク星人には、「トウ星人ですか?」「カイ星人ですか?」「ホク星人ですか?」の3回の質問をします。
カイ星人には、「トウ星人ですか?」「カイ星人ですか?」の2回の質問をするので、2人合わせて4回質問をします。
宇宙船Aは、次の図のように質問をします。

質問した回数は、「トウ星人ですか?」10回「カイ星人ですか?」7回「ホク星人ですか?」5回の合計22回です。
宇宙船Cは、次の図のように質問をします。

質問した回数は、「トウ星人ですか?」10回「カイ星人ですか?」9回「ホク星人ですか?」6回の合計25回です。
質問の順番を入れ替えます。
「トウ星人ですか?」「リク星人ですか?」「ホク星人ですか?」の順番に質問をすると、宇宙船Aでは次のようになります。

このとき、カイ星人は「トウ星人ですか?」「リク星人ですか?」「ホク星人ですか?」の3回の質問をすることになり、最初に示した順番よりも1回多くなります。
また、10人全員へ質問した回数は、「トウ星人ですか?」10回「リク星人ですか?」7回「ホク星人ですか?」3回の合計20回となり、2回少なくなります。
解答 ア③ イ④ ウ② エ⑤ オ④ カ①
問2 二分探索
二分探索は、最初のデータを半分に分けて、そこからさらに半分に分けることを繰り返すことで一致するのか見ていくというものです。
問題文では、「グループ法」と表現されています。
グループ法で宇宙船Aの人に出身星をたずねると、次のようになります。

このとき、宇宙船Aの10人全員への質問回数は「トウカイ銀河から来ましたか?」10回「トウ星人ですか?」5回「ホク星人ですか?」5回の合計20回の質問をすることになります。
それでは、順次法の合計質問回数が最小となるときを考えます。
問題文より、「出身者が多い星から順番に質問した場合に、合計質問回数が最小になる」とあります。
宇宙船Aでは、出身者が多い星はリク星→トウ星→カイ星→ホク星の順です。
この順で質問した場合を、図に示します。

このとき、宇宙船Aの10人全員への質問回数は「リク星人ですか?」10回「トウ星人ですか?」6回「カイ星人ですか?」3回の合計19回の質問をすることになります。
順次法で、5隻の中で合計質問回数が最も少ないのは、トウ星とホク星がともに0人であることから、宇宙船Dです。
詳しくは、次の図で宇宙船B~Eまでの合計質問回数が最も少なくなる場合を示すので、参考にしてください。
宇宙船B

このとき、宇宙船Bの10人全員への質問回数は「カイ星人ですか?」10回「リク星人ですか?」3回「ホク星人ですか?」3回の合計14回の質問をすることになります。
宇宙船C

このとき、宇宙船Cの10人全員への質問回数は「リク星人ですか?」10回「カイ星人ですか?」6回「ホク星人ですか?」3回の合計19回の質問をすることになります。
宇宙船D
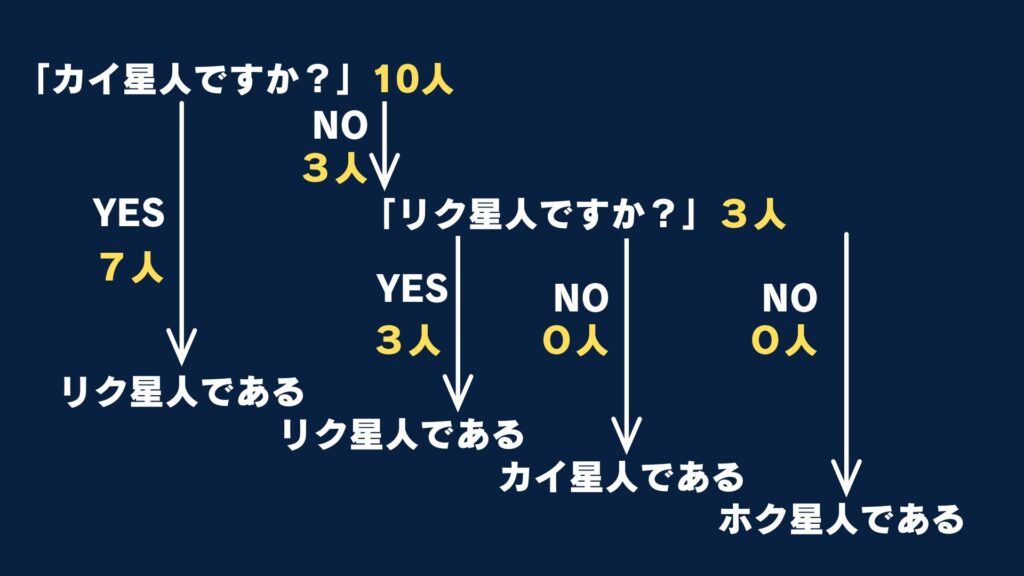
このとき、宇宙船Dの10人全員への質問回数は「カイ星人ですか?」10回「リク星人ですか?」3回の合計13回の質問をすることになります。
宇宙船E

このとき、宇宙船Eの10人全員への質問回数は「カイ星人ですか?」10回「リク星人ですか?」4回「トウ星人ですか?」1回の合計15回の質問をすることになります。
グループ法では、どの10人に出身星をたずねても、合計質問回数は20回と同じになります。
順次法では、質問回数を次のような式で表せます。
- 手順1の質問は、10回
- 手順2の質問は、10ー(出身者が最も多い星の人数)
または(出身者が2番目に多い星の人数)+(出身者が最も少ない星の人数)+(出身者が3番目に多い星の人数) - 手順3の質問は、(出身者が最も少ない星の人数)+(出身者が3番目に多い星の人数)
または、10ー(出身者が最も多い星の人数)+(出身者が2番目に多い星の人数)
合計質問回数は、
10+{10ー(出身者が最も多い星の人数)}+{(出身者が最も少ない星の人数)+(出身者が3番目に多い星の人数)}
=20+(出身者が最も少ない星の人数)+(出身者が3番目に多い星の人数)ー(出身者が最も多い星の人数)
つまり、合計質問回数が20回よりも大きくなる場合は、
(出身者が最も少ない星の人数)+(出身者が3番目に多い星の人数) > (出身者が最も多い星の人数)
です。
解答 キ② ク⓪ ケ① コ⑨ サ③ シ② ス③ セ⓪ (シ・スは順不同)
問3 二段法(2/22更新)
前手順で宇宙船Aを対象としたら、宇宙船Aはリク星人、トウ星人、カイ星人、ホク星人の順で多いことから、X星はリク星、Y星はトウ星となります。
宇宙船ごとに、X星とY星をまとめると次の表のようになります。
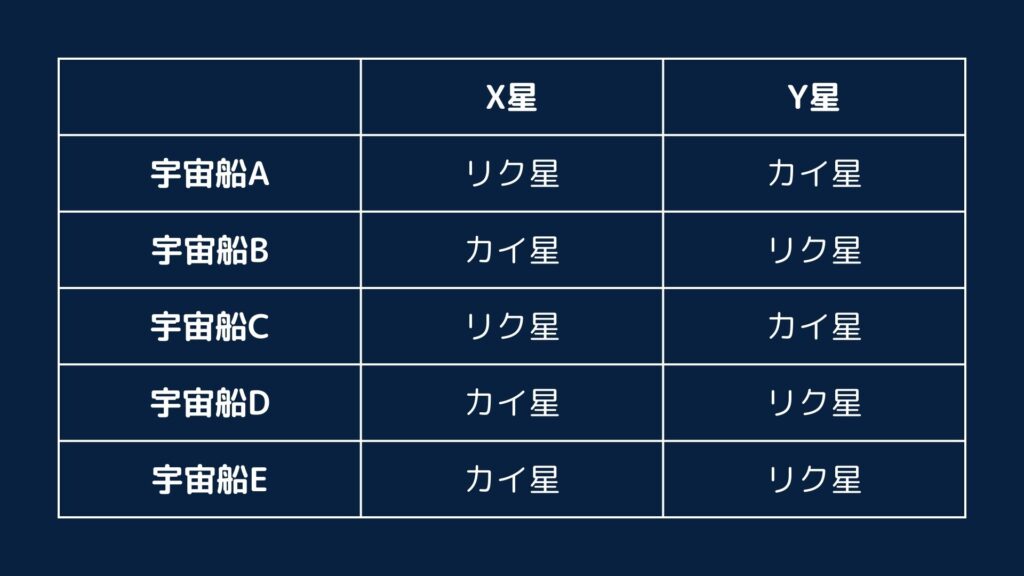
宇宙船Bを対象としたら、X星はカイ星、Y星はリク星なので、後手順のX星人は、宇宙船A・C・D・Eのカイ星人の合計である18人です。
前手順で各宇宙船を対象とした場合の合計質問回数と後手順でのX星人、Y星人、その他の人数の表を埋めると次のようになります。
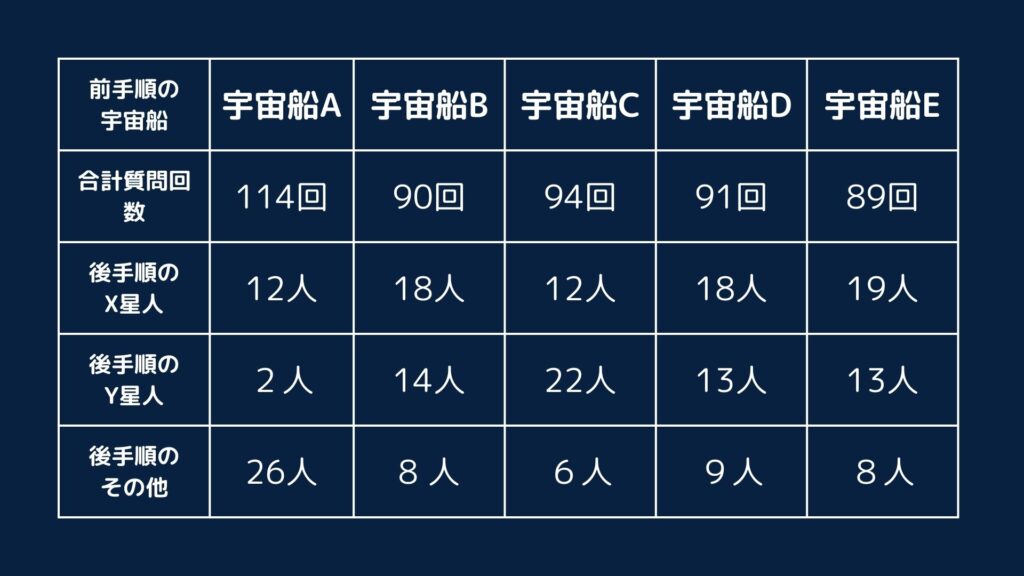
後手順のその他は、前手順の宇宙船以外の4隻の人の合計が40人であることから、40ー(後手順のX星人)ー(後手順のY星人)で求められます。
宇宙船B・D・EはX星はカイ星、Y星はリク星です。
前手順の宇宙船A・Cを比較すると、上の表より宇宙船Cは後手順でその他が少ないことがわかります。
また、表から後手順のX星人の差はなく、後手順のY星人の差が大きいことから、Y星がカイ星となったことが影響していると考えられます。
宇宙船B・Eを比較すると、宇宙船Eでは後手順のX星人が多く、Y星人が少ないことがわかります。
つまり、前手順では宇宙船Eの方がX星人が少なく、Y星人が多いことが合計質問回数の差につながることがわかります。
解答 ソ③ タ⓪ チ① ツ⑧ テ⓪ ト③ ナ② ニ①



コメント