こんにちは。高校情報科の未来予想図です。
情報Ⅰで出てくる「共通鍵暗号方式」と「公開鍵暗号方式」。
正直、こう思いませんか?
・名前がややこしい
・どっちも暗号なら同じじゃない?
・結局、どう違うの?
しかも教科書や資料を見ると、「鍵」「安全」「仕組み」みたいな言葉が並んで、なんとなく分かった気になるけど、説明しろと言われると止まる。
実はこの2つ、使っている計算ルールがまったく違います。
そこが分かると、名前も役割も一気に整理できます。
この記事では、「どんな計算をしているのか」「なぜ2種類あるのか」を、情報Ⅰレベルでシンプルに整理します。
暗号化とは?
暗号化とは、
データを、ある計算ルールに基づいて別の文字列に変換すること
です。
このとき、
- 元のデータ → 平文
- 暗号化されたデータ → 暗号文
- 元に戻す操作 → 復号
と呼びます。
重要なのは、暗号化も復号も「計算」で行われている という点です。
ここでいう「計算」とは、決められたルールと手順に従って処理を行い、同じ入力なら必ず同じ出力になるもの を指します。
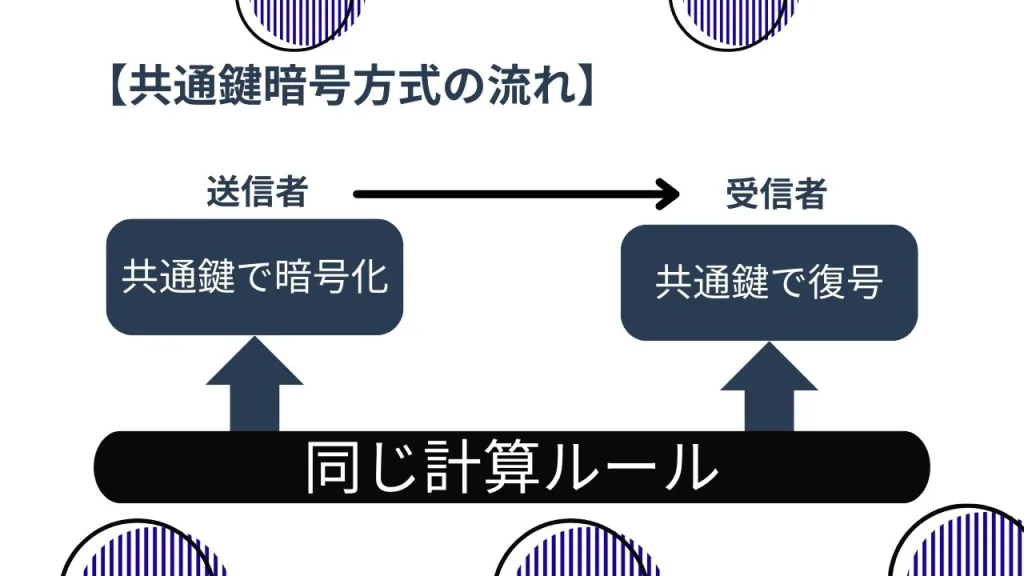
共通鍵暗号方式とは【同じ計算ルールを使う】
共通鍵暗号方式は、
暗号化と復号で、まったく同じ計算ルールを使う方式
です。
仕組み(具体例)
例として、次のような単純な計算ルールを考えます。
- 暗号化:アルファベットを 3文字後ろにずらす
- 復号:アルファベットを 3文字前に戻す
BASE → EDVH
(B→E, A→D, S→V, E→H)この場合、「3」という数値が
暗号化と復号で共通に使われる情報 になります。
共通鍵暗号方式の特徴
メリット
- 計算が単純
- 処理が非常に高速
- 大量のデータ通信に向いている
デメリット
- 暗号化に使う計算ルールを
事前に安全に共有する必要がある
この「ルールの共有」が問題になる点は、情報Ⅰやテストでもよく問われます。
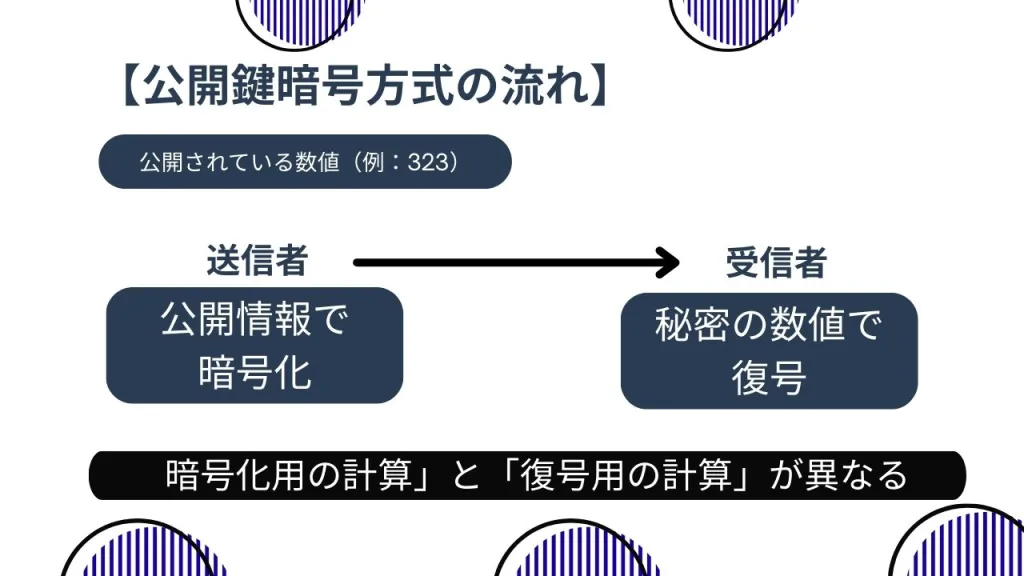
公開鍵暗号方式とは【異なる計算ルールを使う】
公開鍵暗号方式は、
暗号化と復号で、異なる計算ルールを使う方式
です。
ここでは、数学の性質である「一方向の計算は簡単だが、逆算は非常に難しい」という考え方が使われます。
仕組み(素因数分解を使った例)
準備(受信者側)
- 2つの素数
- 17 と 19
- 掛け算して
- 17 × 19 = 323
このとき、
- 323 → 公開してよい情報(公開鍵)
- 17 と 19 → 秘密にしておく情報(秘密鍵)
になります。
暗号化(送信者側)
- 公開されている 323 を使って
- 決められた計算式(べき乗など)でデータを変換
復号(受信者側)
- 暗号文を元に戻せるのは
- 323が 17 × 19 だと知っている人だけ
という仕組みです。
なぜ安全なのか
攻撃者が 323 を入手しても、
- それが
17 × 19
であると見つけ出す必要があります。
実際の暗号では、この数が 数百桁 になります。
- 素因数分解にかかる計算量が非常に大きいため
- 現実的な時間では解読できません
この「計算量の大きさ」が、安全性の根拠です。
共通鍵暗号方式と公開鍵暗号方式の違い【比較】
| 項目 | 共通鍵暗号方式 | 公開鍵暗号方式 |
|---|---|---|
| 計算ルール | 同じ | 異なる |
| 処理速度 | 非常に速い | 遅い |
| 安全性の根拠 | ルールの秘匿 | 逆算の困難さ |
| 主な用途 | 大量通信 | 鍵の受け渡し |
セッション鍵方式【インターネットの実際】
現在のインターネット通信(HTTPSなど)では、2つの方式を組み合わせたハイブリッド方式 である、公開鍵暗号方式の流れが使われています。
流れ
- 公開鍵暗号方式
- 通信開始時に、共通鍵(計算ルール)を安全に送る
- 共通鍵暗号方式
- その後の大量データ通信を高速に行う

情報Ⅰ・テストでの見分け方
- 速さが重要 → 共通鍵暗号方式
- 安全な受け渡しが重要 → 公開鍵暗号方式
- HTTPS・SSL/TLS → 両方使うセッション鍵方式
この3点を押さえると、共通テストや定期試験で迷いにくくなります。
まとめ
- 共通鍵暗号方式
- 同じ計算ルールを使う
- 高速だが、ルールの共有が課題
- 公開鍵暗号方式
- 異なる計算ルールを使う
- 逆算が困難な数学的性質を利用
- 現代の通信
- 両者を組み合わせて安全性と速度を両立
暗号は「秘密の仕組み」ではなく、計算量と計算ルールの設計 によって成り立っています。



コメント